Postupnosť v prírode
Fibonacciho postupnosť v prírode
Výskyt Fibonacciho postupnosti v prírode je taký častý, že to nemožno pokladať za náhodu.
Príklady:
a) počet korunných lupienkov v kvetoch (pozri fotoalbum)
trojlist, šípová ruža, iskerník, nátržník, krvavček, krasuľka, ľalia, kosatec, fialka, astra, sedmokráska, stračonôžka, gailardia, ...
Často sa vyskytujúci počet korunných lupienkov:
5 - orlíček, stračonôžka, fialka
8 - krasuľka, iskerník, stračonôžka, krvavček
13 - chryzantémovka
21 - astra
34, 55, 84 - sedmokráska
b) zoskupenie listov, výhonkov a vetvičiek
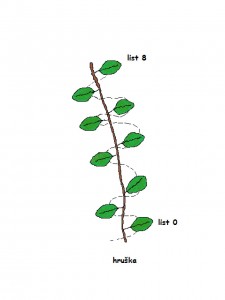
Označme si jeden list na stonke číslom 0 a na myslenej špirále spočítajme listy nad ním, až kým sa nedostaneme presne na úroveň listu 0 (predpokladáme, že nijaký nechýba). Počet listov i obrátok na špirále bude s veľkou pravdepodobnosťou Fibonacciho číslo. Pomer listov k obrátkam sa nazýva filotaxia (z gréc. usporiadanie listov) a býva spravidla jedným z Fibonacciho zlomkov (pomer dvoch susedných Fibonacciho čísel)
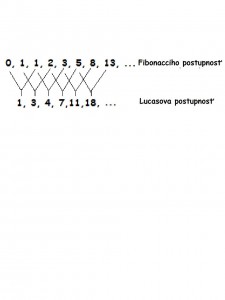
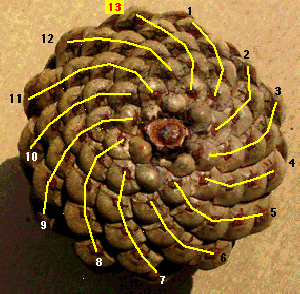
c) počet pravotočivých a ľavotočivých špirál na borovicovej šiške (ide o susedné Fibonacciho čísla - niekedy sú to aj susedné Lucasove čísla, ktoré tvoria Lucasovu postupnosť. 1, 3, 4, 7, 11, 18, ...Platí pre ňu pravidlo fibonacciovskej postupnosti: každé číslo (počnúc tretím) je súčtom predchádzajúcich dvoch. Lucasova postupnosť je pomenovaná podľa Edurda Lucasa, matematika 19. storočia, ktorý študoval rekurentné a dal meno Fibonacciho postupnosti. Medzi týmito dvoma postupnosťami exsistuje následovný vzťah:
d) počet špirál tvoriacich šesťuholníkovú kôru ananásu
Pozoruhodný je i vzťah medzi Fibonacciho postupnosťou a zlatým rezom. Postupnosť zlomkov dvoch susedných čísel Fibonacciho postupnosti totiž striedavo kolíše okolo hodnoty zlatého rezu
.
Limita tejto postupnosti je
.
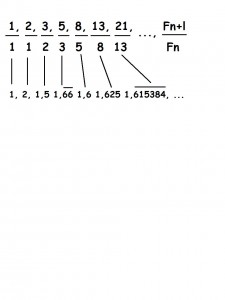Znamená to, že kdekoľvek v prírode sa objaví zlatý rez, zlatý obdĺžnik alebo logaritmická špirála, je tam prítomná i Fibonacciho postupnosť